Introduction to Graph Networks: Directed Networks

On my previous post, we saw what adjacency matrices look like for Undirected Networks. On this one, we’ll take a closer look at Directed Networks and how the structure of the adjacency matrix changes if our edges now point from one node to another.

We can define the adjacency matrix of a directed graph (or digraph, if you are a hipster!) as:

Note: The convention for digraphs on Networkx is the opposite, from i to j. Here we are adopting the mathematical convention.

Notice two things: 1) the direction of the edge runs from the second to the first index (or from the column to the row index, as you prefer), and 2) since the edges are directed, we no longer have a double count of the entries in the matrix. Point (2) means that A is not necessarily symmetric anymore.

Let’s think of an easy digraph (because we are hipsters, of course). Let’s say you and four of your friends are meeting for a post-Covid barbecue. You (column 1, row 1) go by the supermarket to get some burgers and spend $30, while Kevin (column 3, row 3) goes by the liquor store to get some beers and spends $25. There are five of you in total to split the bill equally, so each person will pay $6 for food and $5 for beer.

The transaction graph looks like:

Figure 1: Digraph of money transfers for the barbecue.

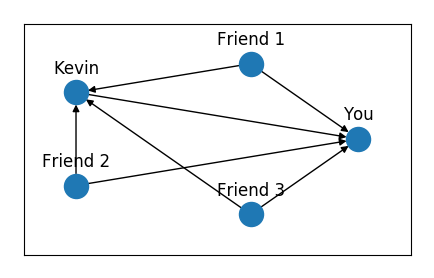
And here is how the transfers will look like in an adjacency matrix:

The transpose of matrix A can be used in Networkx to create the plot above.

So each of the other three friends transfers to you and Kevin the due amounts, and Kevin sends you $1 for the difference $6-$5.

I hope you liked this post. Please hit Like and subscribe to my Medium channel. I hope to bring a lot more about networks in the coming posts.

Let’s learn together! =)